Käesolev võrratuste lahendamise juhend õpetab võrratusi lahendama Microsoft Mathematics (tasuta Microsofti tarkvara) abil ja neid graafiliselt kujutama.

Kui kahe avaldise (arvu) vahel on võrratusmärk (<, >, <= või >= ), siis sellist seost nimetatakse võrratuseks.

Võrratuste ja nende ettekujutamine joonisel annab parema mõistmise võrratuste lahendamisele.

Võrratustel võib olla

a)      üks lahend

b)      mitu või lõpmatu arv lahendeid

c)      lahendid võivad puududa

Võrratuste lahendamine tähendab selle kõigi lahendite leidmist. Ülesanded võivad olla antud tekstiga „leia ühine positiivsus- või negatiivsuspiirkond“. Ka sellisel juhul on tegemist võrratuste lahendamise ülesannetega.

Ruut- ja lineaarne võrratus

On antud järgmised võrratused, mis tuleb lahendada.

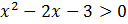
Võrratuse lahendamiseks tuleb see sisestada Mathematics töölehele (Worksheet) viisil, et nende võrratuste vahel on sõna and. See annab programmile teada, et tegemist on kahe võrratuse samaaegse lahendamisega.

Vajuta enter, tulemusena kuvatakse lahendus x > 3. See on mõlema võrratuse ühine piirkond.

Lisaks pannakse lahendatav võrrand sulgudesse, mis algab sõnaga solveIneq ja mille lõpus on „x“. SolveIneq tähendab et lahednatakse võrratust ja x tähistab, et seda lahendatakse muutuja x-suhtes. Mathematics leidis, et antud võrrandis on ainult üks muutuja ning eeldas, et kasutaja soovib leida just seda muutujat.

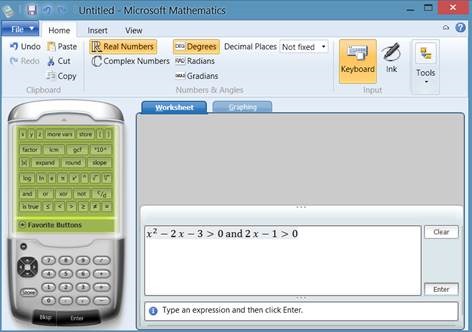
Selleks, et paremini mõista, mida tähendab võrratuse lahendamine graafiliselt, kuva antud tulemus joonisel. Selleks vajuta lingil „plot this inequality“. Joonisel on näha viirutatud ala, mis asub x-teljel number 3-st paremal. See iseloomustabki lahendust x > 3.

Selleks, et aru saada kuidas need kaks võrratust kokku sellise tulemuse annavad, kirjutame need üles võrranditena ja kuvame joonisel.

Töölehele sisesta see võrrand järgmisel kujul:  ja vajuta enter. Tulemusena kuvatakse võrrandi lahendid, kuid praegusel juhul huvitab meid rohkem graafik.

Vajuta lingile „plot both sides of this expression in 2D“. Kõrvutades antud tulemus esialgse võrratuse graafikuga, on näha et mõlemad graafikud on positiivsed alates kolmest, ehk siit jooniselt on lihtne välja lugeda nende võrratuste lahend x > 3.

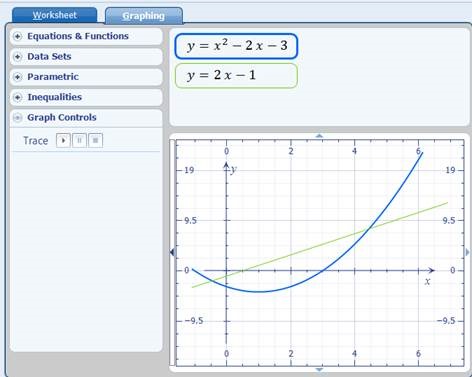
Leia ühine negatiivsuspiirkond

Olgu antud kaks võrrandit ning ülesanne on leida ühine negatiivsuspiirkond.

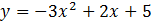
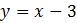
Ülesande tekst nõuab, et need mõlemad võrrandid tuleb teisendada võrratusteks ja seejärel lahendada. Seega ülesande täitmiseks Mathematics abil on tarvis need võrratustena sisestada töölehele järgmisel kujul.

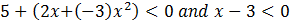
Mõlema võrrandi puhul on = y ära vahetatud võrratusega < 0. Ehk siis leitakse mõlema võrratuse ühised lahendid, mis on väiksemad kui 0.

Sisesta see Mathematics töölehele ja vajuta enter. Mathematics annab lahenduseks 3 varianti: x < -1, x > 5/3 ja x < 3.

Kuvame selle tulemuse graafikul, vajutades lingil „plot this inequality“. Graafiline lahendus on viirutatud ala joonisel.

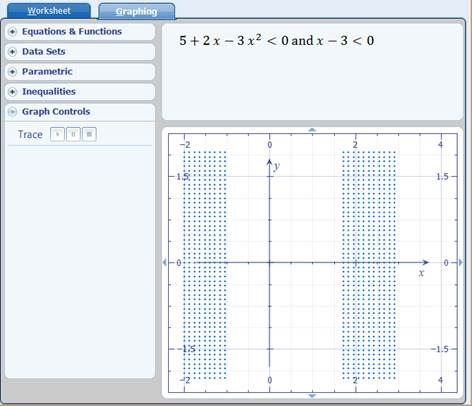
Vaata nüüd kuidas need graafikud joonisel välja näevad ja miks tekkis lahenduseks selline situatsioon.
Sisesta antud võrrandid töölehele ja vajuta enter.

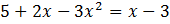
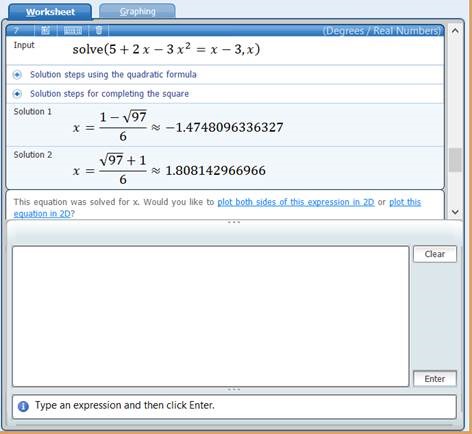
Kuva need graafikud joonisel vajutades linki „plot both sides of this expression in 2D“. Alljärgneval joonisel on näha graafiliselt tulemus mõlema graafiku negatiivsest piirkonnast. See on vasakul pool y-telge alates sellest punktist kus parabool on allpool x-telge. Y-teljest paremal pool on näha väike kolmnurkne piirkond, kus parabool on allpool x telge ning sirge pole veel jõudnud veel x-telge ületada.